
V is the volume of a unit cell, F is the structure factor which depends on the atomic scattering factor, f, of the elements in the phase and the crystal structure of the phase. Other terms in the equation above are the same. This is independent of the diffraction angle. This is about 45 degrees in the Phillips diffractometer using a Cullity suggests using (1+cos 22 aĬos q ), where 2a is the angle the beam isĭiverted in the monochrometer (project the beam path and measure the divergenceĪngle). Polarization occurs in the monochrometer. Phillips camera in lab) this equation is modified since some extent of When a crystal monochrometer is used (as in the The 110 peak of molybdenum can be compared with the 111 peak of copper to determine the relative contributions of the two components. For two peaks, a and b, from two phases the concentration of the two phases can be determined by ratios of equation 12-11,įor the copper and molybdenum mixture the diffraction patterns are indexed using FCC and BCC structures. K is a constant which will cancel in intensity ratios, c a is the concentration of the alpha component, R a is an angular dependent term which is defined in equation 12-10, m m is the absorption coefficient for the mixture,Īppendix 8 p. 408 to 409, equation 14-1),Įquation 12-1 can be simplified for comparison of two reflections which correspond to two different phases in a metal sample, such as a powder mixture of molybdenum and copper. Phase Composition for mixed phase metals (more than one crystal structure):Īs Cullity described on p. In addition, account must be made for the multiplicity of planes in a crystal, variation in thermal broadening with angle and some other factors, see

The intensity from a diffractometer in reflection geometry must be corrected for the angular dependence of absorption/beam profile and for the Lorentz Polarization factor which is also angularly dependent. There are alternative approaches to determination of phase composition including density measurements, thermal analysis and spectroscopy, but XRD remains the most robust and simplest technique so it is of dominant importance. For a multi-phase metal this corresponds to a quantitative analysis of the phase composition. This means that for a material with multiple phases, crystalline/amorphous or several crystalline phases, XRD can be used to determine the volume fraction of these phases. The integrated intensity from a diffraction peak is proportional to the volume fraction of that material in a sample. From the FCC brass structure determine the distance of closest approach and find the number fraction zinc in the brass key.
Vegard's Law predicts a straight line for this plot for brass.Make a plot of closest approach distance versus number fraction zinc, at 0 this is the distance for pure copper determined above and at 1.0 this is the number determined above for copper.Determine the distance of approach for the two patterns ( for HCP this is "a", for FCC this is "a"/ √ (2).Index both crystal structures and determine the lattice parameters.Measure the diffractometer trace for copper and zinc.
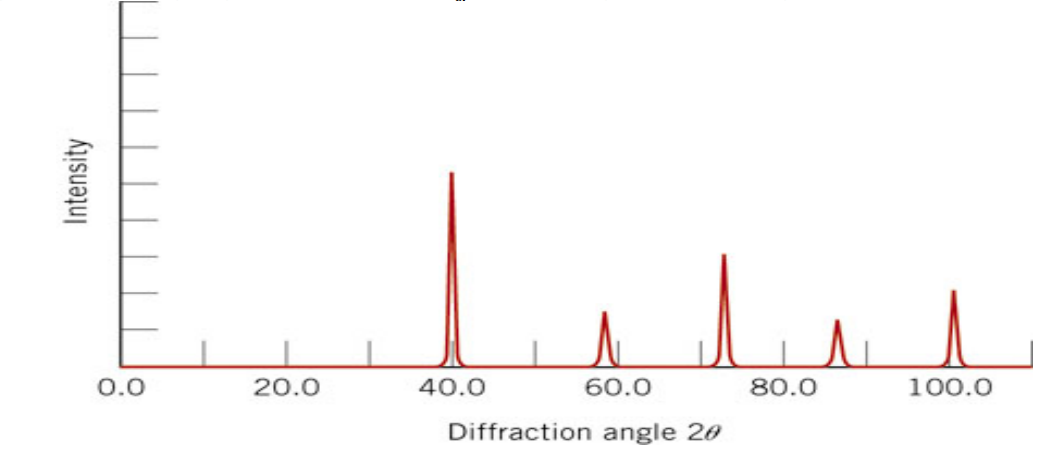
In the powder mixture a calculation of the relative intensity of two peaks will be used to determine the amount of BCC Moly and FCC copper in a mixture containing independent crystals of these two materials. Vegard's Law will be used to determine the zinc content by consideration of the shift in the lattice parameter for the FCC pattern. This lab will involve the analysis of composition of two samples, a brass key, composed of a substitutional solution of zinc in copper (FCC) and a physical mixture of copper (FCC) and molybdenum (BCC) powder. 139 section 4-12 and equation 4-21 for Diffractometer. 12-6, Chapter 14 (Phase Analysis), Chapter 7 (Diffractometer), pp. New Cullity and Stock: Chapter 11, Figure 11-6, Chapter 12 (PhaseĪnalysis), Chapter 6 (Diffractometer), Chapter 4 (Calculated Diffracted Intensity) Objective: To become familiar with use of the diffractometer for quantitative analysis of phases in mixtures/alloys of metals. Lab 6: Diffractometer/Phase Analysis & CompositionĬopper Wire (oriented), Copper Plate (unoriented), Zinc Powder, Brass Key, Moly Powder, Moly/Copper Powder


 0 kommentar(er)
0 kommentar(er)
